Time Series Analysis: A Primer Everything You Need to Know About
In business, you need to know how your business is doing day-to-day. In order to understand the health of your company, many turns to data analytics. Time series analysis can give valuable insight into what has happened over the course of days, weeks, months, or even years.
Time series analysis is a subset of predictive analytics that collects data over regular periods. Such analysis is used by companies to predict their revenue and the impact of major business decisions. In short, it adds more value to business growth.
With this form of analytics, you can learn if your company is making more money during the summer months or at the beginning of the fiscal year. You can also analyze weather data to see if winter storms caused any loss in revenue.
Some questions that time series analysis can answer are: How many customers come into the store every day? How much revenue has the business generated over the last few weeks? What is the probability of rain tomorrow?
It could be helpful in planning future actions, saving money, and ensuring quality.
In this post, we explain what is time series, time series analysis, and its benefits.
Table of Contents
- What is Time Series
- What Is Time Series Analysis And What Is Its Importance?
- Major Components Of Time Series Analysis
- How To Understand A Time Series?
- What Are Stationary And Non-stationary Time Series?
- How To Make A Series Stationary?
- Which Algorithms Can Be Used For Time Series Forecasting?
- What Are The Business Applications Of Time Series Analysis?
- What Are The Objectives Of Time Series Analysis?
What is Time Series?
The sequence of data points indexed or based on time and recorded in successive order is called time-series data points.
What is Time Series Analysis and What is Its Importance?
Time series data analysis is the way to predict time series based on past behavior. Prediction is made by analyzing underlying patterns in the time-series data.
E.g., Predicting the future sales of a company by analyzing its past performance.
Predicting the state of the economy of a country by analyzing various factors affecting it. These series are generally time series, and they contribute to the economy.
The importance of time series analysis for science, industry, and commerce, is as follows:
- The study of past history is necessary for forecasting future events.
- Time series analysis shows why trends exist in past data and how they may be explained by underlying patterns or processes.
- Time series analysis is a basic tool for the analysis of natural systems, which cannot be understood without it. For example, climate cycles and fluctuations in the economy, as well as volcanic eruptions and earthquakes, are examples of natural systems, whose behavior can best be studied using time series analysis.
Time series analysis gives a way to predict the future. It is essential in engineering, finance, business, and the economy to make it easy for investors, customers, or engineers to make the proper decisions.
Forecast new leads with Time Series Analysis
E.g., If we know how the weather will be tomorrow, we will be ready for it before we go outside. Or, If we know the future value of stocks, we can decide whether to invest in or not.
Major Components of Time Series Analysis
Given the discrete nature of time series, the data is often taken from discrete time periods. Here are the 4 major components:
- Trend component
- Seasonal component
- Cyclical component
- Irregular component
1. Trend component: This is useful in predicting future movements. Over a long period of time, the trend shows whether the data tends to increase or decrease. The term “trend” refers to an average, long-term, smooth tendency. Not all increases or decreases have to occur simultaneously. Different sections of time show varying tendencies in terms of trends that are increasing, decreasing, or stable. There must, however, be an overall upward, downward, or stable trend.
2. Seasonal component: The seasonal component of a time series is the variation in some variable due to some predetermined patterns in its behavior. This definition can be used for any type of time series including individual commodity price quotes, interest rates, exchange rates, stock prices, and so on.
In many applications, seasonal components can be represented by simple regression equations. This approach is sometimes referred to as a “seasonalized regression” or a “bimodal regression”
3. Cyclical component: The cyclical component in a time series is the part of the movement in the variable which can be explained by other cyclical movements in the economy.
In other words, this term gives information about seasonal patterns. It is also called the long-period (LP) effect or boom-bust process.
For example, during recessions, business cycles are usually characterized by slower growth rates than before the recession started.
4. Definition of irregular component: The irregular component is the part of the movement in the variable which cannot be explained by cyclical movements in the economy.
In other words, this term gives information about non-seasonal patterns.
This term refers to changes that are not cyclical. These include boom-bust processes, permanent changes in the long-term trend of a variable, or “not seasonally adjusted” information which is not normally found in national income and product accounts (such as depreciation, research and development expenditures, and agricultural subsidies).
How to Understand A Time Series?
The preliminary step in understanding a time series is its visualization. The time-series visualization plots data points on the y-axis w.r.t time on the x-axis. The graph may show some of the following features:
- Trend: A trend is a long-running pattern of time series. It may be upwards or downwards.
- Seasonality: The repetitive patterns at certain times of year are called seasonality. For example, sales of cakes will peak every December in the US because of Christmas.
- Cyclical pattern: The data shows fluctuations at any time of the year.
Residual: The data remaining after removing the above three is called Residual.
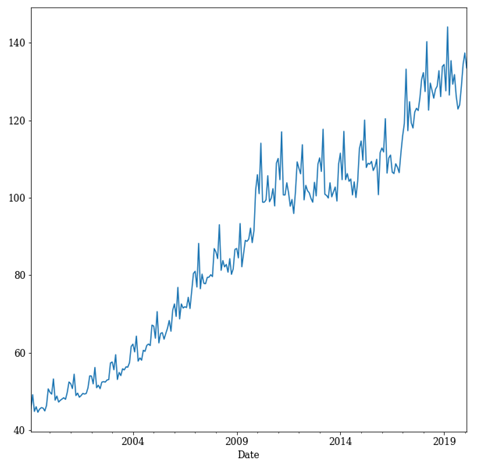
Figure1: Time-series visualization of Index of Industrial Production (IIP) of India.
As shown in Figure 1, there is an upward trend in the graph, and there is a repetitive pattern every year representing seasonality.
Removing trend and seasonality is sometimes important for analyzing a time series as seasonality may hinder getting the actual randomness of the data and give its cyclical pattern in the prediction.
What are Stationary and Non-stationary Time Series?
The time series which has constant mean and variance is called stationary time series. It is recommended to have the stationary time series for better analysis.
The predictions on non-stationary series may give wrong values.
To check whether a series is stationary or not, there are several tests in the literature.
One of them is the Augmented Dickey-Fuller (ADF) test which is a unit root test. Its null hypothesis is that the series is non-stationary.
If the p-value is less than 0.05, the null hypothesis can be rejected, and the series can be considered stationary.
How to Make A Time Series Stationary?
A series can be made stationary by various methods like:
- Difference Transform: Subtracting previous value with current value is called differencing. It is done to remove the dependency of values on time. One can check the differenced series with the ADF test for stationary.
- Second differencing: If the result of the ADF test on the differenced series shows that the series is still non-stationary, then one can subtract the differenced series again.
- Removing trend and seasonality by using HP-filter or band-pass filters and X12 ARIMA analysis.
Is It Necessary to Remove Trend And Seasonality?
No. There are some models like Prophet, SARIMAX, etc., which take care of seasonality while modeling. The basic ARIMA model needs the de-seasonal data.
Which Algorithms Can be Used for Time Series Forecasting?
There are various methods for analyzing time-series data:
- Autoregressive Integrated Moving Average (ARIMA) Models
- Seasonal Autoregressive Integrated Moving Average (SARIMA) Models
- Vector Autoregression (VAR)
- Exponential Smoothing models
- Prophet model.
Once you have the data ready, you can divide the dataset into train and test data, train any of the above models, and test the performance using test data.
How to Compare Performance of Different Models?
The models can be compared on various metrics like:
- MSE (Mean squared error)
- RMSE(Root Mean Squared error)
- MAPE(Mean Absolute Percentage Error) etc.
Out of these metrics, MAPE has generally been considered a good metric for comparing models.
Forecast new leads with Time Series Analysis
What are The Business Applications of Time Series Analysis?
- The forecasting of future values and the identification of trends using linear regression methods, moving averages, variance forecasts, and wavelets
- Short-term time series modeling and ARIMA models
- Seasonal analysis using univariate (trends) and multivariate (stratification) techniques
- Space-time processes
- Measurement uncertainty
- Research using regression models
- Robustness
- Commodity markets
- Forecasting (all levels)
- Fractional statistics
- Finding anomalies
Use-case With Above Mentioned Steps
We have done time-series forecasting for knowing the future revenue of a company.
- We first checked the whole dataset for null values. If there are any null values, those rows are deleted.
- ADF test is done to check if the series is stationary.
- We have used two models for forecasting: The prophet model and Exponential Smoothing.
- The Prophet model takes the seasonal component of the series into consideration. We can mention whether there are seasonal components or not.
- Exponential smoothing has three versions:
- Simple exponential model: This model takes only detrend and deseasonalized data.
- Double exponential smoothing: This model considers only trends for time-series analysis.
- Holt’s winter exponential smoothing: This model considers both trend and seasonality and is the most widely used exponential smoothing method. Its results are more accurate and more diverse.
- Comparison between these models is done based on MAPE, MSE, and RMSE.
- The one which performs better is used for final forecasting.
What are The Objectives of Time Series Analysis?
- To study the trend of the series
- To compute the time-series data
- To create a new data set from the existing one
- To analyze and compare the old and new data sets
- To detect the causality among the variables of the data set
- To study cross-sectional relationships between different types of variables
- To interpret the economic significance of the series data and their relationship with other factors in the economy
Build sentiment analysis models with Oyster
Whatever be your business, you can leverage Express Analytics’ customer data platform Oyster to analyze your customer feedback. To know how to take that first step in the process, press on the tab below.
Liked This Article?
Gain more insights, case studies, information on our product, customer data platform

